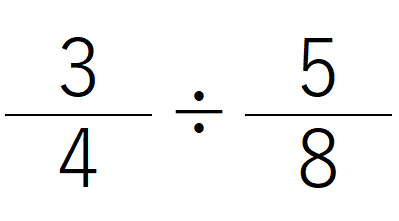分数の計算って、最初はちょっとむずかしそうに感じるかもしれませんよね。特に「分数の割り算」は、「どうして分数をひっくり返すの?」と疑問に思う方も多いです。この記事では、「3/4 ÷ 5/8」という計算を例にして、わかりやすくステップごとに解説します。誰でも理解できるように、図やイメージを使って説明するので、ぜひおうちで一緒に挑戦してみてください。
1. まずは「分数の割り算」の基本ルールを知ろう
分数の割り算には、とても大事なルールがあります。それは、
「割り算をかけ算に変えて、2つ目の分数をひっくり返す」
というルールです。
たとえば、
3/4 ÷ 5/8この計算では、「÷ 5/8」を「× 8/5」に変える必要があります。
なぜひっくり返すのか疑問に思うかもしれませんが、これは「逆数」を使うからです。逆数とは、分数の「分子」と「分母」を入れ替えたもの。5/8の逆数は「8/5」ですね。
では、次に実際の計算の手順を見ていきましょう。
2. 「3/4 ÷ 5/8」をステップごとに計算しよう
ここからは、3/4 ÷ 5/8の計算を、ステップごとに解説していきます。
ステップ1:割り算をかけ算に変える
まず、「割り算」を「かけ算」に変えて、2つ目の分数をひっくり返します。
3/4 ÷ 5/8 → 3/4 × 8/5これで、計算の形がシンプルになりました。
ステップ2:分子同士、分母同士をかける
次に、分子と分母をそれぞれかけます。
分子:3 × 8 = 24
分母:4 × 5 = 20したがって、
24/20という答えが出ます。
ステップ3:分数をできるだけ小さくする(約分)
次に、24/20をできるだけ簡単にしましょう。
24と20の両方を割り切れる数字を探します。
24と20は、どちらも「4」で割り切れます。
24 ÷ 4 = 6
20 ÷ 4 = 5したがって、
6/5これが答えです。
答え:6/5
さらに、「帯分数」に直すと、
1と1/5となります。
3. 分数の割り算のコツを覚えよう!
分数の割り算のコツは次の通りです。
- 割り算をかけ算に変えて、2つ目の分数をひっくり返す
- 分子同士、分母同士をかける
- できるだけ簡単な形にする(約分)
これを覚えておけば、どんな分数の割り算もスムーズにできるようになります。
たとえば、
- 2/3 ÷ 4/5 → 2/3 × 5/4 = 10/12 → 5/6
- 5/6 ÷ 7/9 → 5/6 × 9/7 = 45/42 → 15/14
同じ手順で計算できるので、練習して慣れていきましょう。
4. なぜ分数の割り算は逆数を使うの?
「どうして分数をひっくり返すの?」と疑問に思う子も多いですよね。実はこれ、「割り算」は「何回分入るか」を考える計算だからです。
3/4 ÷ 5/8をイメージしてみましょう。
「3/4の中に、5/8がいくつ入るか?」という意味です。
- 3/4 = 0.75
- 5/8 = 0.625
0.75の中に0.625が何回分入るかを考えると、
0.75 ÷ 0.625 = 1.2これは、6/5と同じですね。
割り算をかけ算に変える理由は、
「割る」という動作が「逆数をかける」ことと同じ意味を持つからなのです。
これで、分数の割り算に対する「なぜ?」もスッキリしたのではないでしょうか。
まとめ
「3/4 ÷ 5/8」は「6/5」という答えになりました。計算の手順は次の通りでした。
- 割り算をかけ算にして、2つ目の分数をひっくり返す
- 分子同士・分母同士をかける
- 答えをできるだけ簡単にする
この方法を知っていれば、分数の割り算ももう怖くありません!
さあ、他の分数でも練習してみましょう!