中学数学で学ぶ「反比例」は、比例と並んでとても重要な概念です。
反比例とは、一方の数値が大きくなると、もう一方の数値が小さくなるという関係を表しています。例えば、仕事のスピードと作業時間、蛇口の水量と水がたまる時間など、日常生活でも多く見られる関係です。
この記事では、反比例の基本的な意味から公式、グラフの描き方、日常生活での例、さらには勉強のコツまでをわかりやすく解説します。数学が苦手な人でもイメージしやすいように具体例を交えていますので、ぜひ最後までお読みください。
反比例とは何か?
反比例とは、「ある数量が大きくなると、もう一方の数量が小さくなる」という関係を表す数学的な用語です。
数学的には次のように表されます。
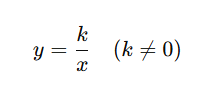
ここで、
- x:説明する数(独立変数)
- y:対応する数(従属変数)
- k:比例定数(常に一定の値)
例えば「xが2倍になるとyは1/2倍になる」というように、逆の動きをするのが反比例の特徴です。
比例との違い
比例と反比例は混同されやすいですが、その関係性は正反対です。
- 比例(y=ax ):xが増えればyも増える。グラフは直線。
- 反比例(y=k/x):xが増えればyは減る。グラフは双曲線。
比例が「一緒に伸び縮みする関係」だとすれば、反比例は「片方が伸びると片方が縮む関係」と考えると覚えやすいです。
反比例のグラフ
反比例をグラフに表すと、特徴的な曲線になります。

日常生活における反比例の例
反比例は数学の世界だけでなく、身近な生活の中にも数多く存在します。
- 作業の人数と作業時間
人数が2倍になれば、かかる時間は半分になる。 - 蛇口の水量と水がたまる時間
水の出る量が多ければ、同じ容器が満たされる時間は短くなる。 - スピードと移動時間
同じ距離を走る場合、速さが2倍になれば時間は半分になる。 - 印刷速度と印刷にかかる時間
プリンターの性能が上がれば、1枚あたりの印刷時間は短くなる。
こうして考えると、反比例は「効率やスピード」に関わる場面でよく登場することがわかります。
反比例の応用問題
反比例を理解するためには、実際の問題を解いてみるのが効果的です。
例題1
ある作業を1人でやると12時間かかります。これを3人で行った場合、何時間かかるでしょうか。

例題2
蛇口から毎分2リットル水を出すと、容器が30分で満水になります。毎分5リットル出した場合、何分で満水になるでしょうか。

学習のコツ
反比例を理解するためのコツをいくつか紹介します。
- 積が一定になることを意識する
𝑥 × 𝑦 = 𝑘 という形で考えるとイメージしやすい。 - 比例と対比して覚える
比例=「一緒に増える」、反比例=「逆に動く」と対比させると整理しやすい。 - 身近な例で考える
水・速度・人数などの例を使って考えると定着しやすい。
反比例が使われる分野
数学だけでなく、反比例は多くの分野で応用されています。
- 物理学:光の明るさは距離の2乗に反比例する(逆二乗の法則)。
- 化学:気体の体積と圧力は反比例する(ボイルの法則)。
- 経済学:需要と価格の関係は反比例に近い動きをする。
- 工学:電気回路のオームの法則では、抵抗が大きいと電流は小さくなる。
このように、反比例は自然界や社会現象を理解するうえでも重要な法則です。
よくある間違い
反比例を学ぶ際に生徒が陥りやすい間違いも紹介します。
- 比例と混同する:直線のグラフを描いてしまう。
- 原点を通ると考える:反比例のグラフは原点を通らない。
- x=0を代入してしまう:0で割ることはできないので、x=0は定義されない。
これらに注意して理解を深めることが大切です。
まとめ
反比例は「一方が増えると他方が減る」という関係を表す数学の基本概念です。
公式は y=k/x、グラフは双曲線の形になります。
日常生活でもスピードと時間、人数と作業時間など、多くの場面で登場します。
比例と反比例をセットで理解し、積が一定になる関係を意識すれば、数学の理解がより深まります。
さらに物理や化学、経済学など幅広い分野で応用される重要な考え方でもあります。
数学を勉強している方はもちろん、日常生活に役立てたい方も「反比例」を意識してみると、新しい発見があるかもしれません。
