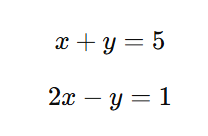連立方程式は、中学数学で学ぶ大切な単元の一つです。二つ以上の方程式を同時に満たす解を求めるための考え方であり、数学だけでなく理科や経済学、さらにはプログラミングやデータ分析の分野でも広く活用されています。しかし、最初に学ぶときには「なぜ二つの式を使うのか」「どうやって計算すればよいのか」と戸惑う人も多いのではないでしょうか。この記事では、連立方程式の基本から代表的な解き方(加減法・代入法・グラフによる方法)を丁寧に解説し、実際の例題を通して理解を深めていきます。さらに、応用的な考え方や実生活での活用シーンについても紹介します。
連立方程式とは何か
連立方程式とは、複数の方程式を同時に満たす解(変数の値)を求める問題です。もっとも基本的な形は、未知数が2つ(例えば xxx と yyy)で、方程式も2本あるものです。
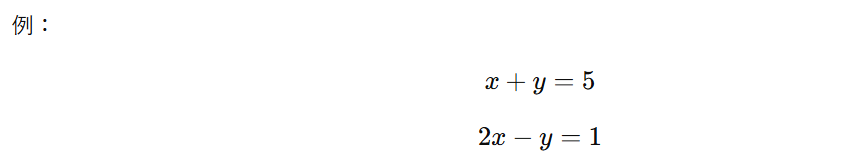
この場合、「xとyの値を同時に決める」ことが求められます。1本の式だけでは解は無数に存在しますが、2本の式を組み合わせることで解が一つに定まります。これは、2本の直線の交点を求めるイメージと考えると理解しやすいでしょう。
連立方程式を解く3つの基本方法
連立方程式にはいくつかの解き方がありますが、中学校で学ぶ代表的な方法は次の3つです。
- 加減法
- 代入法
- グラフによる方法
それぞれの手法を順に解説します。
加減法での解き方
加減法は、二つの式を「足す」あるいは「引く」ことで、一方の文字を消去する方法です。
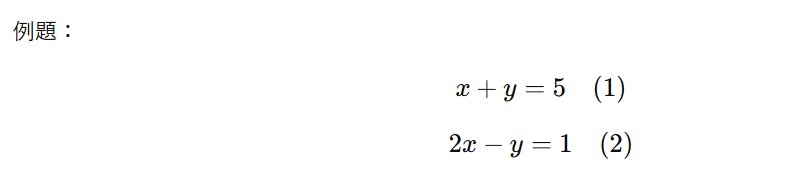
手順:
- (1)と(2)を足すと、3x=63x = 63x=6 となり、x=2 が求まります。
- この値を(1)に代入すると、2+y=52 なので y=3。
答え:(x,y)=(2,3)
加減法のポイントは、「yを消すには足せばいいのか、xを消すには何倍して引けばいいのか」を考えることです。慣れてくると素早く計算できるため、試験でもよく使われます。
代入法での解き方
代入法は、一方の式から文字を一つ表し、その式をもう一方に代入する方法です。
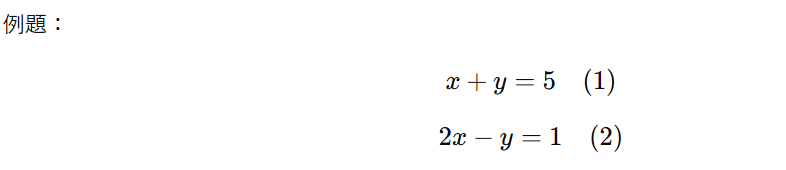
手順:
- (1)から y=5−xy = 5 と変形。
- これを(2)に代入すると、2x−(5−x)=1。
- 整理すると、3x−5=1、したがって x=2。
- (1)に戻して y=3。
答え:(x,y)=(2,3)
代入法は計算がやや複雑になる場合がありますが、論理的に「一つの変数にまとめていく」方法なので理解しやすいです。
グラフで解く方法
連立方程式をグラフに表すと、それぞれの方程式は「直線」として描けます。二つの直線が交わる点の座標が解となります。

- 1本目の直線は、y=−x+5
- 2本目の直線は、y=2x−1
- これを座標平面に描くと、交点が(2,3)になります。
視覚的に理解できるため、連立方程式の「意味」を理解するのに役立ちます。ただし試験では時間がかかるため、練習段階で活用するのがよいでしょう。
連立方程式の応用問題
連立方程式は単なる計算だけでなく、文章題として出題されることが多いです。
例:りんごとみかんの値段
「りんご2個とみかん3個で310円、りんご1個とみかん2個で170円。りんごとみかんの値段はいくらか?」
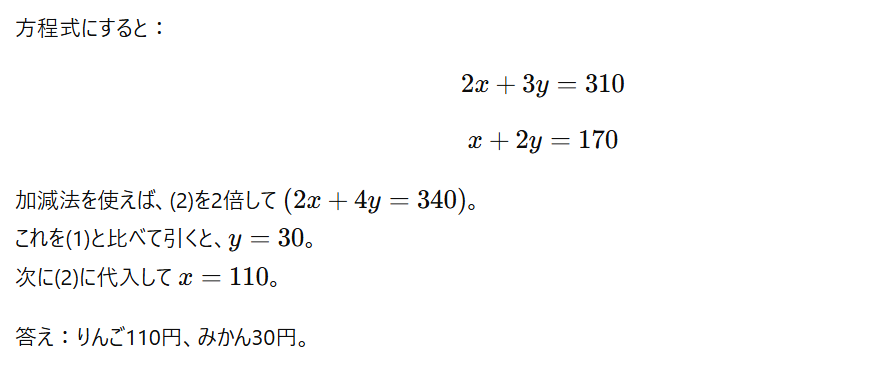
このように実生活の問題を数式化して解く力が身につくと、数学の面白さがぐっと増します。
3元連立方程式
高校に進むと、未知数が3つの「3元連立方程式」も登場します。
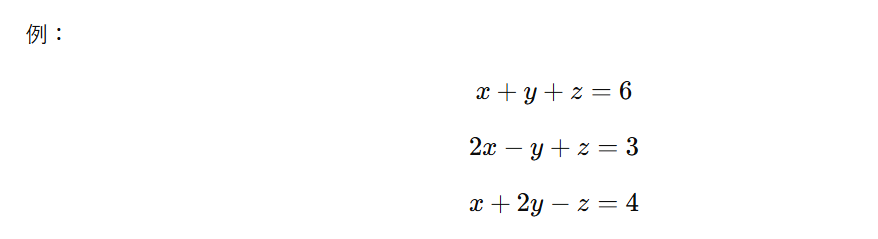
手順は基本と同じで、加減法や代入法を組み合わせて文字を一つずつ消去していきます。慣れないうちは計算が煩雑ですが、整理して進めれば必ず解けます。
連立方程式と行列の関係
さらに数学を進めていくと、連立方程式は「行列」を使って表すことができます。行列の考え方を導入すると、大量の方程式をコンピュータで一気に解くことが可能になります。これは、データ解析やAIの分野でも重要な考え方です。
実生活での活用シーン
連立方程式は、学校の勉強だけでなく以下のような場面でも役立ちます。
- 経済学:需要と供給の関係を数式で表すとき
- 物理学:複数の力が働く運動を解くとき
- プログラミング:アルゴリズムで最適解を求めるとき
- 日常生活:買い物や料金計算で条件を整理するとき
「複数の条件から最適な答えを見つける」という意味で、連立方程式は思考の基本ツールともいえます。
まとめ
連立方程式は、「二つ以上の方程式を同時に満たす解を求める」ための計算方法です。基本的な解き方は 加減法・代入法・グラフ の3つであり、応用すれば文章題や実生活の問題解決にもつながります。さらに数学を進めれば行列やコンピュータ計算とも結びつき、幅広い分野で役立つ知識となります。
勉強の最初は「計算が面倒」と感じるかもしれませんが、解き方のパターンを身につければスムーズに解けるようになります。ぜひ例題を繰り返し練習して、自分の得意な方法を見つけてみましょう。