数学の世界において「比例」と「反比例」は、関数を理解するうえで最初のステップとなる重要な概念です。特に中学生の数学で登場するこの内容は、身の回りの現象とも深く結びついており、生活の中にも数多くの例があります。この記事では、比例と反比例の違いや特徴、式の作り方、グラフの形まで、わかりやすく丁寧に解説していきます。これから関数の世界に入る方にも、復習をしたい方にも役立つ内容となっています。
比例とは?──同じ割合で増える関係
まずは「比例」から説明しましょう。比例とは、ある量が変化すると、それに合わせてもう一つの量も一定の割合で変化する関係をいいます。
たとえば、りんご1個が100円だとします。このとき、りんごを2個買えば200円、3個なら300円と、りんごの数が増えれば代金も一定の割合で増えていきます。
このように、
- ある量 xxx に対して
- それに比例して変化する量 yyy があるとき、
次のような関係式で表されます。
y = ax
ここで、
- aaa は「比例定数」と呼ばれ、1個あたりの価格のような「1単位あたりの変化量」を意味します。
【比例の特徴】
- x=0x = 0x=0 のとき、必ず y=0y = 0y=0(原点を通る)
- グラフにすると、直線になる
- 比例定数 aaa が大きいほど、グラフは急な傾きになる
反比例とは?──一方が増えればもう一方が減る関係
「反比例」とは、一方の量が大きくなると、もう一方の量が小さくなるような関係です。
例を挙げましょう。ある作業を終えるのに必要な時間は、手伝う人数が増えるほど短くなります。
たとえば1人でやれば4時間かかる仕事も、2人なら2時間、4人なら1時間で終わる。これが反比例の関係です。
反比例の関係は次の式で表されます。
y = a / x
ここでも
- aaa は定数(反比例定数)で、関係を表す決まった値です。
【反比例の特徴】
- xxx が大きくなると yyy は小さくなる(逆も同様)
- x=0x = 0x=0 のとき、定義できない(分母が0になるため)
- グラフにすると、双曲線(2つの曲線が原点を避けて向き合う形)になる
比例と反比例の違いを整理しよう
| 項目 | 比例 | 反比例 |
|---|---|---|
| 関係式 | y=axy = axy=ax | y=a/xy = a/xy=a/x |
| グラフの形 | 原点を通る直線 | 双曲線 |
| x=0x = 0x=0 のとき | y=0y = 0y=0 | 定義できない |
| 変化の仕方 | xxx が増えると yyy も増える | xxx が増えると yyy は減る |
| 比例定数 | 傾き(変化の割合) | 定積(積が一定) |
実生活での例を見てみよう
【比例の例】
- 商品の値段(1個100円 → 3個で300円)
- 距離と時間(一定の速さで進むとき、時間に比例して距離が増える)
【反比例の例】
- 作業人数と時間(人数が増えると、必要な時間が減る)
- 水流と時間(水の流れが速いほど、水がたまる時間は短くなる)
グラフで見ると一目瞭然!
【比例のグラフ】

【反比例のグラフ】

関数としての捉え方:比例・反比例は「関数」の第一歩!
比例も反比例も、「ある数 xxx に対して、決まったやり方で yyy が決まる」関係です。
このように、1つの値に対応してもう1つの値が決まる関係のことを数学では**「関数」**といいます。
関数の基本は「入力 → 出力」の関係です。
比例や反比例は、以下のように表せます。
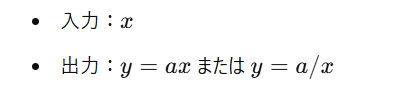
このように、比例と反比例を理解することは、関数全体の理解への第一歩なのです。
中学数学のポイント:比例・反比例を使いこなすために
式の立て方に慣れよう
文章題から比例や反比例の式を立てる練習をしてみましょう。
「○○に比例する」と書かれていれば「y=axy = axy=ax」、
「○○に反比例する」と書かれていれば「y=a/xy = a/xy=a/x」という式を立てることができます。
グラフとの関係を理解しよう
グラフを書く練習をすると、視覚的に比例や反比例の関係がつかみやすくなります。点をプロットして線や曲線を描いてみるのがおすすめです。
まとめ
比例と反比例は、関数という考え方の入り口としてとても大切な単元です。
- 比例は「一定の割合で一緒に増える関係」
- 反比例は「一方が増えれば他方が減る関係」
この2つをしっかり理解することで、数学の世界がぐっと広がります。日常の中でも見つけられる身近な関係を探して、楽しく学んでみましょう!

