数学には「連続」を扱う分野と「離散」を扱う分野があります。私たちが学校で学ぶ微積分や解析学は「連続量」を対象にしていますが、情報科学やデータ処理の世界では「離散的な構造」を理解することが欠かせません。これを体系的に学ぶのが「離散数学」です。近年では、コンピュータサイエンス、暗号理論、AI、ネットワーク解析など幅広い分野で応用されており、情報化社会を支える基盤知識の一つといえます。この記事では、離散数学の基本概念から、代表的なテーマ、そして実生活やビジネスへの応用例までをわかりやすく解説していきます。
離散数学とは何か
離散数学とは「数えられる対象」を扱う数学の総称です。連続的に変化する量(例えば時間や距離)を扱う解析学とは異なり、個数や組合せ、有限の構造を対象とします。
代表的に含まれるテーマは以下のようなものです。
- 集合論
- 論理学
- グラフ理論
- 組合せ論
- 数論(特に整数論)
- オートマトンや形式言語
これらは一見バラバラに見えますが、コンピュータサイエンスの理論的基盤を作り、現代社会で欠かせない応用につながっています。
集合と写像
集合論は離散数学の出発点です。集合とは「要素を一つにまとめたもの」を指し、数学的対象を整理する基本の道具です。
例えば、自然数の集合 {1,2,3,… } や、曜日の集合 {月,火,…,日} などが例に挙げられます。
また、写像(関数)は集合と集合の対応関係を表すもので、プログラミングにおける「入力と出力の対応」に直結します。データベースやアルゴリズムにおいて、集合や写像の考え方が常に使われています。
論理と命題
コンピュータの動作を理解するうえで「論理学」は欠かせません。
命題とは「真か偽かが判定できる文」です。例えば「2は偶数である」は命題ですが、「今日はいい天気だ」は主観的要素を含むため数学的命題とは言えません。
命題論理では「AND(かつ)」「OR(または)」「NOT(否定)」などの論理演算を組み合わせて推論を行います。これはそのままプログラミングの条件分岐や、デジタル回路における基本動作に対応しています。
ブール代数もこの分野に含まれ、0と1で情報を処理するコンピュータの根幹を支えています。
グラフ理論
グラフ理論は離散数学の中でも特に応用範囲が広い分野です。
グラフは「点(頂点)と線(辺)」で表現される構造で、SNSの友達関係や道路網、ネットワーク接続などをモデル化できます。
例えば、「最短経路問題」はナビアプリで利用されており、「巡回セールスマン問題」は物流の効率化や配送計画に直結します。
近年では、グラフ理論を応用した「グラフニューラルネットワーク(GNN)」がAI研究で注目され、化学分子の構造解析やソーシャルネットワークの解析にも活用されています。
組合せと確率
組合せ論は「いくつの並べ方・取り出し方があるか」を数える学問です。宝くじやカードゲーム、暗号鍵の強度計算など、実生活に密接に関わっています。
例えば、52枚のトランプから5枚を選ぶ方法の数は組合せで表されます。
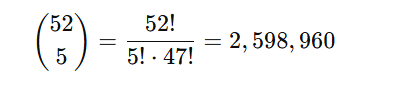
つまり、ポーカーの手役の組み合わせは約260万通り存在するのです。
また、確率論と組み合わせることで、リスク管理や機械学習の理論基盤を支えています。
数論と暗号
数論は整数の性質を扱う分野で、離散数学の重要な柱です。特に素数の研究は暗号技術に直結します。
RSA暗号は「大きな数を素因数分解するのは計算的に難しい」という性質を利用して安全性を確保しています。現代のインターネット通信、オンラインショッピングや電子決済は、まさに数論の応用の上に成り立っているのです。
また、合同算やモジュラ計算はハッシュ関数やデータ圧縮技術にも応用されます。
オートマトンと形式言語
コンピュータの「計算可能性」を理解するために、オートマトン理論や形式言語が必要です。
有限オートマトンはシンプルな計算モデルですが、正規表現の基盤となっており、検索システムやテキスト処理に応用されています。
また、チューリングマシンは「どのような計算が理論的に可能か」を定義する抽象的な機械で、アルゴリズムの限界や人工知能研究の哲学的議論にも関わっています。
離散数学とコンピュータサイエンス
離散数学はコンピュータサイエンスの必修科目といえる分野です。
- データ構造(木、グラフ、集合)
- アルゴリズム設計(探索、最適化)
- プログラムの正しさの検証(論理)
- セキュリティ(暗号)
- AIと機械学習(確率・グラフ)
これらの理論を知らずにコンピュータを扱うことは、基礎を知らずに家を建てるようなものです。実装力を磨くと同時に、離散数学を理解することでより強固な技術力を得られます。
実生活での応用例
離散数学は日常のさまざまな場面に潜んでいます。
- スケジュール調整:グラフの彩色問題(会議室割り当てなど)
- 暗号通信:インターネットのセキュリティを守る数論
- 物流:組合せ最適化による配送ルート短縮
- 検索エンジン:グラフ理論と確率論を応用したランキング
- データベース:集合論と論理に基づいた設計
私たちが日々便利に利用しているサービスの裏には、必ず離散数学の理論が存在しているのです。
学習のすすめ方
離散数学は抽象的に見えますが、具体例と結びつけることで理解が進みます。学習の手順としては以下がおすすめです。
- 集合と論理の基礎を学ぶ
- 証明技法(背理法、数学的帰納法)を身につける
- グラフ理論や組合せ論に挑戦する
- 数論や暗号への応用を学ぶ
- 実際のアルゴリズムやプログラムに当てはめてみる
また、プログラミング言語を併用して実験すると、抽象的な理論が具体的なコードとして理解できるようになります。
まとめ
離散数学は、コンピュータやデータ社会の基盤を支える学問分野です。集合、論理、グラフ、組合せ、数論、オートマトンといった幅広いテーマが含まれ、現代の情報技術に直結しています。
一見すると難解に見えますが、日常生活やビジネスの中にも応用が多く、学ぶほどに「世界を数学的に捉える視点」が養われます。これからプログラミングやAI、データサイエンスに取り組む人にとって、離散数学はまさに必修科目といえるでしょう。

